TEA加密算法

TEA

以加密解密速度快，实现简单著称

TEA算法使用64bit(8byte)的明文分组和128bit(16byte)的密钥，它使用Feistel分组加密框架，采用迭代的形式，推荐的迭代轮数是64轮，最少32轮。

简单的说就是，TEA加密解密是以原文以8字节（64位bit）为一组，密钥16字节（128位bit）为一组，（char为1字节，int为4字节，double为8字节）

该算法使用了一个DELTA常数作为倍数，它来源于黄金分割数与232的乘积，以保证每一轮加密都不相同。但δ的精确值似乎并不重要，这里TEA把它定义为 δ=「(√5 - 1)231」，这个δ对应的数指就是0×9E3779B9，但有时该常数会以减法的形式出现，-0x61c88647=0×9E3779B9。

代码实现

解密只需要将加密逆过来即可

#include <iostream>

//加密函数
void encrypt(uint32_t* v, uint32_t* k) {
    uint32_t v0 = v[0], v1 = v[1], sum = 0, i;             
    uint32_t delta = 0x9e3779b9;                            
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];    
    for (i = 0; i < 32; i++) {                             
        sum += delta;
        v0 += ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
        v1 += ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
    }                                                      
    v[0] = v0; v[1] = v1;
}


//解密函数
void decrypt_tea(uint32_t* v, uint32_t* k) {
    uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, i;     
    uint32_t delta = 0x9e3779b9;                           
    uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];    
    for (i = 0; i < 32; i++) {                                  
        v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);
        v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);
        sum -= delta;
    }                                                          
    v[0] = v0; v[1] = v1;
}

识别特征：

• 标准DELTA常数（魔数）
• 密钥为16字节（4个DWORD）
• 加密轮数为16/32/64轮
• 加密结构中存在左4右5移位以及异或运算（v(2^n)==v<<n*）
• 加密结构中存在轮加/减相同常数的语句

对抗方式：

• 修改魔数
• 修改轮数
• 修改轮加/减魔数的位置

XTEA

TEA 算法被发现存在缺陷，作为回应，设计者提出了一个 TEA 的升级版本——XTEA。

XTEA是TEA的扩展，也称做TEAN，它使用与TEA相同的简单运算，同样是一个64位块的Feistel密码，使用128位密钥，建议64轮，但四个子密钥采取不正规的方式进行混合以阻止密钥表攻击。它增加了更多的密钥表，移位和异或操作等。

代码实现

#include <iostream>
void encrypt(uint32_t * v , uint32_t * k) {
    u32 v0 = v[0], v1 = v[1];
    u32 k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
    u32 sum = 0;
//xTEA

    for (int i = 0; i < rounds; i ++) {
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + k[sum & 3]);
        sum += delta;
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + k[(sum >> 11) & 3]);
    }

    v[0] = v0;
    v[1] = v1;
}

void decrypt(uint32_t * v , uint32_t * k) {
    u32 v0 = v[0], v1 = v[1];
    u32 k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];
    u32 sum = rounds * delta;


//xTEA
    for (int i = 0; i < rounds; i ++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + k[(sum >> 11) & 3]);
        sum -= delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + k[sum & 3]);
    }

    v[0] = v0;
    v[1] = v1;
}

识别特征：

• 同TEA
• 加密结构中存在右移11位并&3的运算

例题练习：[HNCTF 2022 WEEK2]TTTTTTTTTea

该题的逻辑很清晰，不难分析出flag=v5=v9，而v9又赋值给v4[8]v4[13]，由下面的for循环可以得知，v4[0]v4[5]分别赋值给v4[8]~v4[13]，所以经过加密后的数据已知，目标是将加密算法逆过来，找到密钥，得到加密前的v4数据。

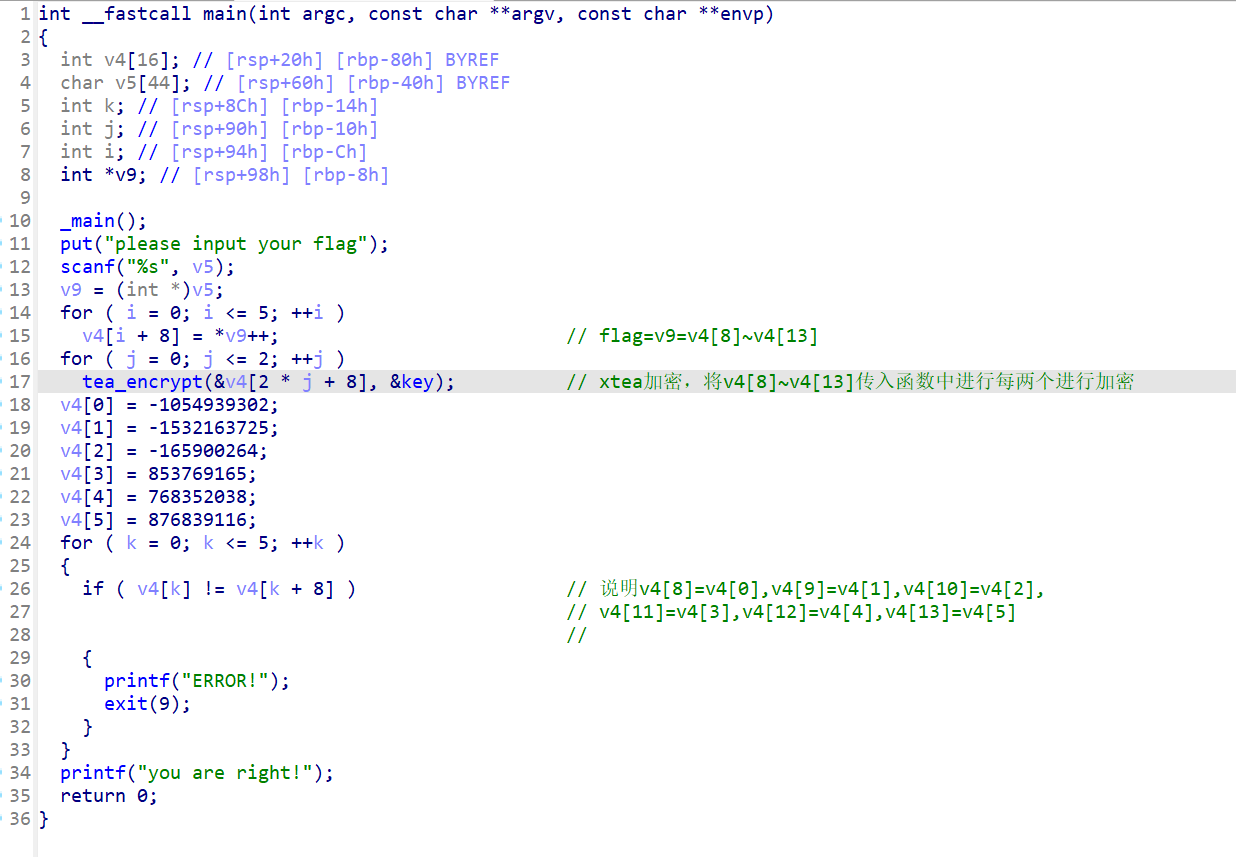
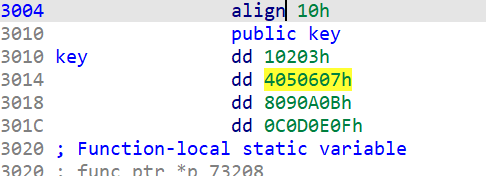
有明显的特征，加密结构中存在右移11位并&3的运算，与标准的xtea进行比对，可以知道，delta=0x61c88647，a2是key，现在要找到key，双击key，点进去就行，可以看到key的值。key要求为8字节，有4位，按d可以将其变成8字节的。

exp：

#include <stdio.h>
#include <stdint.h>
void decrypt (uint32_t* v, uint32_t* k) {
    long delta=0x61C88647; //加密后的delta


    for (int j = 0; j < 6; j += 2)
    {
        unsigned int v0 = v[j];//v6
        unsigned int v1 = v[j+1];//v5
        unsigned int v6 = 0;
        long sum = -delta*32;

    for (int i=0; i < 32; i++)
    {
        v1 -= (((v0 >> 5) ^ (16 * v0)) + v0) ^ (k[((sum >> 11) & 3)] + sum);
        sum += delta;
        v0 -= (((v1 >> 5) ^ (16 * v1)) + v1) ^ (k[(sum & 3)] + sum);
    }
    v[j]=v0; v[j+1]=v1;
    }
}

int main()
{
    uint32_t enflag[] = {0xC11EE75A, 0xA4AD0973, 0xF61C9018, 0x32E37BCD, 0x2DCC1F26, 0x344380CC};
    uint32_t key[] = {0x00010203,0x04050607,0x08090A0B,0x0C0D0E0F};


        decrypt(enflag, key);
        printf("%s",enflag);
    return 0;
}

解出flag：NSSCTF{Tea_TEA_TeA_TEa+}

XXTEA

XXTEA，又称Corrected Block TEA，是XTEA的升级版 ，设计者是Roger Needham, David Wheeler。其实现过程要比前两种的算法略显复杂些，加密的明文不再是64bit（两个32位无符号整数），并且其加密轮数是由n，即待加密数据个数决定的。

#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))
#include <stdio.h>
#include <stdint.h>

void xxtea(uint32_t* v, int n, uint32_t const*key)
{
    uint32_t y, z, sum;
    unsigned p, rounds, e;
    if (n > 1)            //encrypt
    {
        rounds = 6 + 52 / n;
        sum = 0;
        z = v[n - 1];
        do
        {
            sum += DELTA;
            e = (sum >> 2) & 3;
            for (p = 0; p < n - 1; p++)
            {
                y = v[p + 1];
                z = v[p] += MX;
            }
            y = v[0];
            z = v[n - 1] += MX;
        }
         while (--rounds);
    }
    else if (n < -1)      //decrypt
    {
        n = -n;
        rounds = 6 + 52 / n;
        sum = rounds * DELTA;
        y = v[0];
        do
        {
            e = (sum >> 2) & 3;
            for (p = n - 1; p > 0; p--)
            {
                z = v[p - 1];
                y = v[p] -= MX;
            }
            z = v[n - 1];
            y = v[0] -= MX;
            sum -= DELTA;
        }
         while (--rounds);
    }
}

//test
int main()
{
    //两个32位无符号整数，即待加密的64bit明文数据
    uint32_t v[2] = {0x12345678,0x78563412};
    //四个32位无符号整数，即128bit的key
    uint32_t k[4] = {0x1,0x2,0x3,0x4};
    //n的绝对值表示v的长度，取正表示加密，取负表示解密
    int n = 2;


    printf("Data is :%x %x\n",v[0],v[1]);

    xxtea(v,n,k);
    printf("Encrypted data is :%x %x\n",v[0],v[1]);

    xxtea(v,-n,k);
    printf("Decrypted data is :%x %x\n",v[0],v[1]);
    return 0;
}

XXTEA算法的解密同样只是对加密算法的数据处理顺序进行倒置，同时加法改减法（减法改加法）。

识别特征：

• 轮数一般为 rounds = 6 + 52 / n，比较明显，一般很少改动

总结

xxtea算法的例题很少见，感觉见的最多的是xtea及其变形。每一道题都有不同，不能死套着脚本，应该根据题的不同而进行修改，比如轮数，魔数，异或等的一些改变。

识别特征：

• 可能存在针对64bit以及128bit数字的操作（输入的msg和key）

• 存在先进行位移，然后异或的类似操作（(z>>5^y<<2)这类混合变换）

• 前面一个复杂的混合变换的结果可能会叠加到另一个值上，两者相互叠加（Feistel 结构）

• 获取密钥的时候，会使用某一个常量值作为下标（key[(sum>>11) & 3]）

• 会在算法开始定义一个delta，并且这个值不断的参与算法，但是从来不会受到输入的影响（delta数值，根据见过的题目中很少会直接使用0x9e3779b9）

  借鉴于一位大佬写的博客https://www.kn0sky.com/?p=279